Kunci jawaban MATEMATIKA Kelas 8 halaman 176 - 177

Kunci jawaban MATEMATIKA SMP Kelas 8 halaman 176 - 177 Bab IV

Bismillahirrohmannirrohim

Kunci jawaban MATEMATIKA SMP kelas VIII halaman 176 - 177 Bab 4 merupakan alternatif Jawaban dari soal-soal Buku MATEMATIKA Kelas 8 SMP/MTs Bab 4 Persamaan Garis Lurus semester 1. Jawaban yang kami berikan hanya berupa jawaban alternatif saja, sebagai referensi bagi adik-adik . Rajin lah belajar dan membaca dari berbgai sumber agar khasanah pengetahuannya bertambah. Sebaiknya  adik-adik mencoba alternatif  jawaban sendiri. 

Dengan adanya pembahasan kunci jawaban seperti ini diharapkan dapat membantu peserta didik Kelas VIII SMP/MTs dalam menjawab soal-soal baik sebagai Tugas Individu maupun Kelompok. Dan Juga dapat menjadi Referensi untuk soal ulangan seperti soal penilaian harian, soal penialain tengah semester , soal penilaian akhir tahun, maupun tugas pekerjaan rumah (PR). Semoga bermanfaat bagi adik adik.

Kunci jawaban MATEMATIKA Kelas 8 Halaman 176 - 177 Bab 4 Semester 1

Ayo Kita Berlatih 4.5

1. Tentukan apakah garis berikut sejajar dengan sumbu-X atau sumbu-Y?

Jawaban :

a) Garis p yang melalui A(8, –3) dan B(5, –3). sejajar sumbu-x karena memiliki nilai Y yang sama.

b) Garis q yang melalui C(6, 0) dan D(–2, 0). sejajar sumbu-x karena memiliki nilai Y yang sama.

c) Garis r yang melalui E(–1, 1) dan F(–1, 4). sejajar sumbu-y karena memiliki nilai X yang sama.

d) Garis s yang melalui G(0, 6) dan H(0, –3). berhimpitan sumbu-y karena memiliki nilai X keduanya sama dengan 0.

e) Garis t yang melalui I(2, –4) dan J(–3, –4). sejajar sumbu-x karena memiliki nilai Y yang sama.

2. Tentukan apakah pasangan garis berikut sejajaratau saling tegak lurus?

Jawaban :

a) Gradien garis a = (y2 - y1) / (x2 - x1)

= (3 - (-3)) / (11 - 7)

= (3 + 3) / 4

= 6/4

= 3/2

Gradien garis b = (y2 - y1) / (x2 - x1)

= (6 - 0) / (-5 - (-9))

= 6 / (-5 + 9)

= 6 / 4

= 3/2

Karena gradien garis a = gradien garis b, maka pasangan garis tersebut Saling Sejajar.

b) Gradien garis m = (y2 - y1) / (x2 - x1)

= (0 - 5) / (0 - 3)

= -5 / -3

= 5/3

Gradien garis n = (y2 - y1) / (x2 - x1)

= (3 - 0) / (-5 - 0)

= 3 / -5

= -3/5

Karena gradien garis m jika dikali dengan gradien garis n hasilnya = -1, maka pasangan garis tersebut Saling Tegak Lurus.

3. Kemiringan garis m adalah 2. Tentukan kemiringan garis n jika:

Jawaban :

a) Gradien m = 2 sejajar dengan garis n, karena sejajar maka :

Gradien n = gradien m = 2

Jadi, kemiringan garis n adalah 2.

b) Gradien m = 2 tegak lurus dengan garis n, karena tegak lurus maka :

Gradien n = -1 / gradien m = -1/2

Jadi, kemiringan garis n adalah -1/2.

4. Diketahui sebuah garis lurus memiliki persamaan y = 2x + 5.

Jawaban :

Gradien garis y = 2x + 5, y = mx + c, maka m1 = 2.

a) y = 2x - 8,

y = mx + c

m2 = 2

karena m1 = m2 = 2, maka Sejajar

b) 4x - 2y + 6 = 0

a = 4, b = -1, c = 0

m2 = -a/b = -4/-2 = 2

karena m1 = m2 = 2, maka Sejajar

c) 3y = 6x – 1

6x -3y - 1 = 0

a = 6, b = -3, c = -1

m2 = -a/b = -6/-3 = 2

karena m1 = m2 = 2, maka Sejajar

d) 7x – 14y + 2 = 0

a = 7, b = -14, c = 2

m2 = -a/b = -7/-14 = 1/2

karena m1 x m2 = 2 x 1/2 = 1, maka Tidak Tegak Lurus ataupun Sejajar

5. Coba buktikan apakah persamaan garis lurus berikut saling tegak lurus.

Jawaban :

a) 2y = 2x – 3

y = x -3/2

y = mx + c

m1 = 1

y = –x + 3

y = mx + c

m2 = –1

Karena m1 x m2 = 1 x -1 = -1, maka kedua garis Saling Tegak Lurus

b) 3x + y = 7

y = -3x + 7

y = mx + c

m1 = -3

3x – 6y = 7

6y = 3x - 7

y = 1/2x -7/6

m2 = 1/2

Karena m1 x m2 tidak sama dengan -1, maka kedua garis Tidak Saling Tegak Lurus

c) (4x + 6)/3 = 4y

12y = 4x + 6

y = 1/3x + 1/2

y = mx + c

m1 = 1/3

3x + 4y + 2 = 0

a = 3, b = 4, c = 2

m2 = -a/b = -3/4

Karena m1 x m2 tidak sama dengan -1, maka kedua garis Tidak Saling Tegak Lurus

6. Diketahui persamaan garis lurus 3x + 4y – 5 = 0 dan 6x + 8y – 10 = 0.

Jawaban :

Gradien garis 3x + 4y - 5 = 0 :

a = 3, b = 4, c = -5

m1 = -a/b = -3/4

Gradien garis 6x + 8y - 10 = 0

a = 6, b = 8, c = -10

m2 = -a/b = -6/8 = -3/4

Karena m1 = m2, maka kedudukan dua persamaan garis tersebut adalah Saling Sejajar.

7. Diketahui fungsi f(x) = 3x + 7 dan g(x) = 6x – 8. Bagaimanakah kedudukan dari dua fungsi tersebut?

Jawaban :

f(x) = 3x + 7

m1 = 3

g(x) = 6x - 8

m2 = 6

Karena m1 tidak sama dengan m2, maka kedudukan dua fungsi tersebut adalah Saling Berpotongan.

Grafik f(x) + g(x)

y = f(x) + g(x)

y = 3x + 7 + 6x – 8

y = 9x - 1

Titik yang dilalui (0,-1) , (1,8) , (2,17)

8. Diketahui fungsi f(x) = 2x + 5 dan g(x) = –1/2 x – 6. Bagaimanakah kedudukan dari dua fungsi tersebut?

Jawaban :

f(x) = 2x + 5

m1 = 2

g(x) = -1/2x - 6

m2 = -1/2

Karena m1 x m2 = 2 x -1/2 = -1, maka kedudukan dari dua fungsi tersebut adalah Saling Tegak Lurus

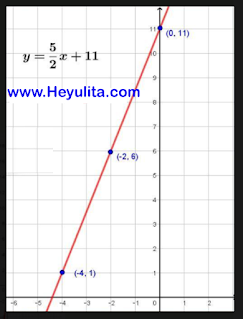
Grafik f(x) - g(x)

y = f(x) - g(x)

y = 2x + 5 - (-1/2x - 6)

y = 2x + 5 + 1/2x + 6

y = 5/2x + 11

Titik yg dilalui (-4,1) , (-2,6) , (0,11)

Demikian Pembaca Kunci Jawaban MATEMATIKA SMP Kelas 8 halaman 176 - 177 Bab 4 buku siswa kelas VIII SMP/MTs kurikulum 2013.

Tentunya ini hanya sebagai alternatif saja  Untuk itu diperlukan kebijakan Bapak/Ibu untuk memilah dan menggunakan nya.

Akhir kata semoga bermanfaat, dan jangan lupa memberikan saran dan komentar positif anda pada Kolom yang tersedia untuk kemajuan website ini.