Kunci jawaban MATEMATIKA Kelas 9 halaman 92, 93

Kunci jawaban MATEMATIKA SMP Kelas 9 halaman 92, 93 Bab II

Bismillahirrohmannirrohim

Kunci jawaban MATEMATIKA SMP kelas IX halaman 92, 93 Bab II merupakan alternatif Jawaban dari soal-soal Buku MATEMATIKA Kelas 9 SMP/MTs Bab II Persamaan dan Fungsi Kuadrat semester 1. Jawaban yang kami berikan hanya berupa jawaban alternatif saja, sebagai referensi bagi adik-adik . Rajin lah belajar dan membaca dari berbagai sumber agar khasanah pengetahuannya bertambah. Sebaiknya  adik-adik mencoba alternatif  jawaban sendiri.

Dengan adanya pembahasan kunci jawaban seperti ini diharapkan dapat membantu peserta didik Kelas IX SMP/MTs dalam menjawab soal-soal baik sebagai Tugas Individu maupun Kelompok. Dan Juga dapat menjadi Referensi untuk soal ulangan seperti soal penilaian harian, soal penialain tengah semester , soal penilaian akhir tahun, maupun tugas pekerjaan rumah (PR). Semoga bermanfaat bagi adik adik.

Kunci jawaban MATEMATIKA Kelas 9 Halaman 92, 93 Bab II Semester 1

a. y = 1/2 x²

Langkah pertama kita tentukan titik-titik yang dilalui ½ x²

Contoh alternatif jawaban :

x y = ½ x²    (x,y)

-4 1/2.(-4)² = 8 (-4,8)

-2    ½.(-2)² = 2 (-2,2)

0 ½.0² = 0 (0,0)

2 ½.2² = 2 (2,2)

4 1/2.4² = 8 (4,8)

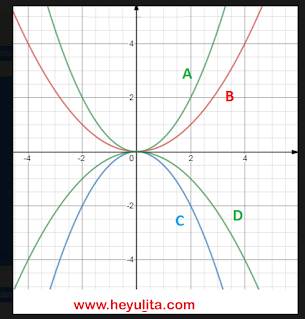
Gambar grafik kuadrat

1b. y = ¼ x²

x y = ¼ x² (x,y)

-4 ¼.(-4)² = 4 (-4,4)

-2 ¼ .(-2)² = 1 (-2.1)

0 ¼.0² = 0 (0,0)

2 ¼.2² = 1 (2,1)

4 ¼.4² = 4 (4,4)

1c. y = -1/2 x²

x y = -1/2 x² (x,y)

-4 -1/2.(-4)² = -8 (-4,-8)

-2 -1/2.(-2)² = -2 (-2,-2)

0 -1/2.0² = 0 (0,0)

2 -1/2.2² = -2 (2,-2)

4 -1/2.4² = -8 (4,-8)

1.d. y = -1/4x²

x y = -1/4x² (x,y)

-4 -1/4.(-4)² = -4 (-4,-4)

-2 -1/4.(-2)² = -1 (-2,-1)

0 -1/4.0² = 0 (0,0)

2 -1/4.2² = -1 (2,-1)

4 -1/4. 4² = -4 (4,-4)

2. Dari Soal 1, apa yang dapat kamu simpulkan mengenai grafik y = ax2 dengan |a|

< 1 dan a ≠ 0?

Jawaban : Jika dibandingkan dengan grafik y = x2 maka grafik y = ax2 akan lebih “gemuk”

3a. y = x² + 3x + 2

x y = x² + 3x + 2 (x,y)

-4 (-4)² + 3.(-4) + 2 = 6 (-4,6)

-3 (-3)² + 3.(-3) + 2 = 2 (-3,2)

-2 (-2)² + 3.(-2) + 2 = 0 (-2,0)

-1 (-1)² + 3.(-1) + 2 = 0 (-1,0)

0 0² + 3.0 + 2 = 2 (0,2)

1 1² + 3.1 + 2 = 6 (1,6)

2 2² + 2.3 + 2 = 12 (2,12)

3.b. y = x²- 3x + 2

x y = x²- 3x + 2 (x,y)

-2 (-2)²- 3.(-2) + 2= 12 (-2,12)

-1 (-1)² -3.(-1) + 2 = 6 (-1,6)

0 0² - 3.0 + 2 = 2 (0,2)

1 1² - 3.1 + 2 = 0 (1,0)

2 2² - 3.3 + 2 = 0 (2,0)

3 3² - 3.3 + 2 = 2 (3,2)

4 4² - 3.4 + 2 = 6 (4,6)

3.c. y = x² + 5x + 6

x y = x² + 5x + 6 (x,y)

-5 (-5)² + 5.(-5) + 6 = 6 (-5,6)

-4 (-4)² + 5.(-4) + 6 = 2 (-4,2)

-3 (-3)² + 5.(-3) + 6 = 0 (-3,0)

-2 (-2)² + 5.(-2) + 6 = 0 (-2,0)

-1 (-1)² + 5.(-1) + 6 = 2 (-1,2)

0 0² + 5.0 + 6 = 6 (0,6)

1 1² + 5.1 + 6 = 12 (1,12)

3.d. y = x² - 5x + 6

x y = x² - 5x + 6 (x,y)

-1 (-1)² - 5.(-1) + 6 = 12 (-1,12)

0 0² - 5.0 + 6 = 6 (0,6)

1 1² - 5.1 + 6 = 2 (1,2)

2 2² - 5.2 + 6 = 0 (2,0)

3 3² - 5.3 + 6 = 0 (3,0)

4 4² - 5.4 + 6 = 2 (4,2)

5 5² - 5.5 + 6 = 6 (5,6)

4. Dari Soal 3, apa yang dapat kamu simpulkan mengenai perbandingan grafik y = ax2 + bx + c dengan y = ax2 – bx + c?

Jawaban : Grafik y = ax2 – bx + c merupakan pencerminan terhadap sumbu-x grafik y = ax2 + bx + c

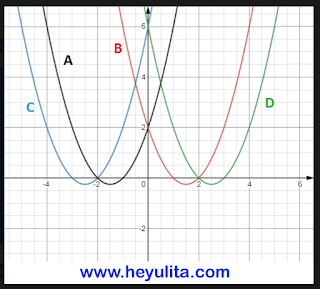
5. Gambarkan grafik fungsi kuadrat berikut.

a. y = x2 + 4x + 2 

b. y = -x2 + 2x + 3

c. y = x2 – 5x + 5

d. y = –2x2 + 4x + 5

Jawaban :

 

6. Dari soal nomor 5, tentukan titik puncak tiap-tiap grafik. Tentukan pula hubungan titik puncak grafik fungsi y = ax2 + bx + c dengan nilai -b/2a.

Jawaban : Titik puncak terjadi pada saat x = -b/2a

7. Apakah mungkin grafik fungsi kuadrat tidak memotong sumbu-x? Jelaskan alasanmu.

Jawaban : Mungkin, dari suatu grafik kungsi kuadrat yang memotong sumbu-x kita dapat menggesernya ke atas atau ke bawah untuk mendapatkan grafik fungsi kuadrat yang tidak memotong sumbu-x. Contoh: y = x2 memotong sumbu-x , tetapi y = x2 + 4 tidak memotong sumbu-x.

8. Apakah mungkin grafik fungsi kuadrat tidak memotong sumbu-y? Jelaskan alasanmu.

Jawaban : Tidak. Karena grafik fungsi kuadrat f(x) pasti memotong sumbu-y pada saat x = 0. Diperoleh f(0) = c, sehingga memotong sumbu-y pada titik koordinat (0, c).

9. Apakah mungkin grafik fungsi kuadrat memotong sumbu-x pada tiga titik koordinat berbeda? Jelaskan alasanmu.

Jawaban : Tidak. Karena f(x) = ax2 + bx + c memiliki akar-akar maksimal sebanyak 2, sehinga grafiknya memotong sumbu-x maksimal sebanyak 2 kali.

10. Apakah mungkin grafik fungsi kuadrat memotong sumbu-y pada dua titik koordinat berbeda? Jelaskan alasanmu.

Jawaban : Tidak. Cukup jelas dari jawaban soal no 8 bahwa nilai f(0) adalah tunggal.

Demikian Pembaca Kunci Jawaban MATEMATIKA SMP Kelas 9 halaman 92, 93  Bab II buku siswa kelas IX SMP/MTs kurikulum 2013.

Tentunya ini hanya sebagai alternatif saja  Untuk itu diperlukan kebijakan Bapak/Ibu untuk memilah dan menggunakan nya.

Akhir kata semoga bermanfaat, dan jangan lupa memberikan saran dan komentar positif anda pada Kolom yang tersedia untuk kemajuan website ini.